Metoda Monte Carlo to temat dla mnie ważny, ponieważ prace nad nim były jednym z przełomów w mojej karierze zawodowej. Rozwiązywanie zadań z metod numerycznych są dla mnie fascynujące i utwierdzają mnie w przekonaniu, że matematyka w programowaniu ma sens (nie samym CRUD-em programista żyje). Jednym z takich zagadnień dotyczących całkowania się zajmiemy. Chodzi oczywiście o tytułową metodę Monte Carlo. Postaram się wyjaśnić następujące kwestie:
- Czym w ogóle jest metoda MC?
- Jakie może mieć zastosowania?
- Jak ją zaimplementować?
- Co ma wspólnego liczba PI z metodą MC?
- Czym jest igła Buffona?
Chcę zaznaczyć, że temat jest poważny i ciężki. Wiele osób ma awersję, słysząc magiczne słowo matematyka. Uważam, że dziedzina ta ma swoje piękne strony i postaram się ją trochę pokazać w tym wpisie.
Zatrzymaj się!
Książki to obowiązkowa pozycja dla każdego zainteresowanego programowaniem!
Jest to zdecydowanie jedno z najlepszych źródeł do nauki programowania! Zyskasz przewagę w branży IT i osiągniesz dużo jako deweloper.
Słowem wstępu
Metoda Monte Carlo to zagadnienie, nad którym pracował jednocześnie zespół węgierskiego matematyka Johna von Neumanna oraz polski matematyk Stanisław Ulam. W różnych definicjach spotkać się można raz z jednym, raz z drugim matematykiem i ciężko stwierdzić, kto w pierwszej kolejności opracował i wykorzystał do obliczeń metodę MC. Pierwsze oficjalne wzmianki pojawiły się w roku 1949 w artykule zatytułowanym „The Monte Carlo method”.
Wciąż jest dla mnie źródłem nieustającego zdziwienia, że kilka znaków nagryzmolonych na tablicy lub na kartce papieru może zmienić bieg ludzkich spraw.
Stanisław Ulam
Metoda Monte Carlo swoją nazwę zawdzięcza nazwie miasta w księstwie Monako. Miasto to słynie z gier hazardowych, które cechują się losowym charakterem. Główną ideą metody jest rozwiązywanie pewnych problemów matematycznych za pomocą losowych wyborów. Podstawy teoretyczne były znane od dawna, jednak możliwości stosowania metody MC nabrały sensu wraz z rozwojem komputerów (dlatego też postanowiłem zmierzyć się z tematem).
Przykład ogólny
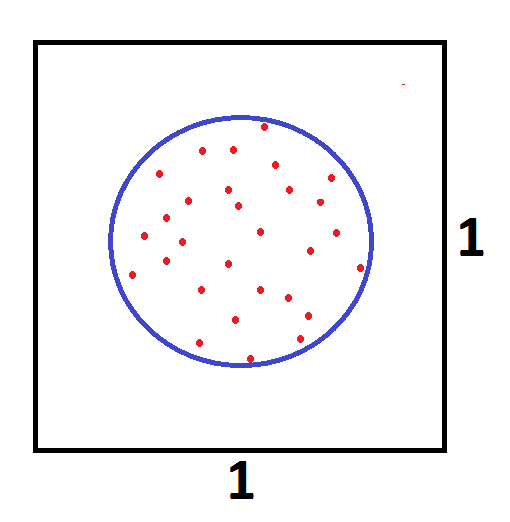
Aby zobrazować sposób, w jaki działa metoda MC posłużę się rysunkiem. Zadaniem będzie obliczenie pola figury S, która to figura znajduje się wewnątrz kwadratu o boku 1. Warto wspomnieć, że figura może przybrać dowolny kształt, ważne by była wewnątrz kwadratu o boku a.
Mając taką konstrukcję geometryczną, kolejnym krokiem będzie wylosowanie N punktów, dowolnie rozmieszczonych wewnątrz kwadratu. Na przykład rysunek poniżej zawiera 41 takich punktów (czerwone kropki). Mając informację o liczbie kropek znajdujących się wewnątrz figury S (kropek tych jest dokładnie 25) mamy możliwość oszacować z pewnym prawdopodobieństwem pole figury S. Pole takie wyliczamy, mnożąc pole powierzchni kwadratu przez liczbę punktów wewnątrz figury S i dzieląc otrzymany wynik przez liczbę wszystkich kropek. Daje nam to 1 * 25 / 41 = 0,6097. Wiedząc, że dokładne pole figury S wynosi dokładnie 0,65, możemy zauważyć, że wynik bardzo nie odbiega od rzeczywistości i w wielu przypadkach wynik taki będzie zadowalający.

Przykład tarczy
Oczywistym jest fakt, że im więcej takich „punktów” umieścimy w kwadracie, tym nasze szacowanie będzie dokładniejsze. Do tego typu obliczeń idealnie nadają się współczesne komputery. Podam jeszcze jeden przykład z błędnym podejściem do szacowania.
Wyobrazić można sobie taki eksperyment na podstawie tarczy do gry w popularną barową grę zwaną dart. Mając koło wewnątrz kwadratu, po oddaniu dużej liczby rzutów i policzeniu liczby rzutek, które trafiły w koło, możemy oszacować jego pole powierzchni. Podejście wydaje się słuszne, jednak jest jeszcze jeden aspekt. Chodzi mianowicie o „równomiernie rozmieszczone” punktów. Podczas gry w dart, trafiając na dobrego gracza, możemy mieć problem z obliczeniami, ponieważ osoba taka może rzucać w tarczę wszystkie swoje rzutki. Pomiar wtedy będzie błędny, bo zasugeruje, że koło ma takie samo pole jak kwadrat.
Patrz rysunek poniżej.
Metoda Monte Carlo i liczba π
Jednym z ciekawszych zastosowań metody Monte Carlo jest próba oszacowania przybliżonej wartości liczby Pi, czyli policzenia liczby punktów, które trafiły w koło wpisany w kwadrat. Wydaje się to prostym zadaniem jednak aby to zrobić, potrzebujemy pewnych informacji na temat pola powierzchni koła.
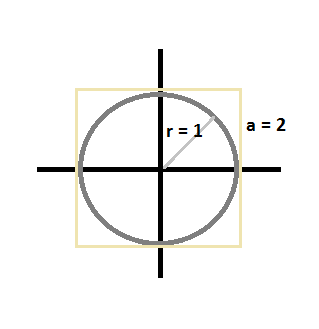
Po pierwsze zobacz rysunek poniżej. Widać tam kwadrat o boku długości a = 2 oraz koło, które posiada taką samą średnicę. Wynika z tego, że jego promień r = 1. Teraz wystarczy przypomnieć sobie, jak wygląda wzór na pole koła:
Pole koła = π * r2
Gdy pod r podstawione zostanie 1, to pole koła wyniesie π. Logicznie rzecz ujmując, im więcej pomiarów (punktów) zostanie wykorzystanych do oszacowania pola powierzchni koła, tym dokładniejszy otrzymamy wynik. Wystarczy zgodnie z regułą opisywaną na początku artykułu zebrać wszystkie punkty, które trafiły w koło, przemnożyć te punkty przez pole kwadratu i na końcu podzielić wynik przez liczbę wszystkich pomiarów, które zostały użyte.
Implementacja
Poniższy kod pozwoli nam w przybliżeniu przedstawić wartość π. Na wejście programu prosimy użytkownika o wprowadzenie liczby losowych punktów (linie 9-10). W kolejnej linii deklarujemy zmienną int, która przechowa sumę punktów, które trafiły w koło. Wartości valX oraz valY przechowywać będą wylosowane liczby z zakresu od 0 do 2 i reprezentować odpowiednio pozycję na osi X, oraz osi Y w układzie kartezjańskim. Dwie następne linie również dotyczą deklaracji. Linia 13 to obiekt Random, który dalej będzie używany do wywołania metody NextDouble. Metoda będzie odpowiedzialna za wylosowanie randomowej wartości. ReturnVal przechowa natomiast wynik.
Główne ciało metody rozpoczyna się instrukcją warunkową, która sprawdza, czy liczba losowych punktów jest mniejsza od 3. Gdyby była to oznacza, że szacunek byłby zbyt niedokładny i prezentowany komunikat, że nie jest możliwe wyznaczenie przybliżonej wartości PI (linie 16-17). Gdy program przejdzie dalej, natrafi na pętle, której to pętli zadaniem jest wyznaczenie wartości valX oraz valY z przedziału od 0 do 2 (funkcja rand.NextDouble() zwraca wartości od 0 do 1, dlatego dodatkowo następuje mnożenie razy 2). Czas na gościa głównego programu — jest nim równanie okręgu. Jeżeli pamiętasz ze szkoły średniej, równanie okręgu ma następujący wzór:
(? – ? )2 + (? − ?)2 = ?2
We wzorze a oraz b to 1. Promień tego koła również wynosi 1. X oraz Y to odpowiednio wartości valX oraz valY. Już teraz wzór nabiera sensu i można go przedstawić w następującej postaci:
![]()
Odwzorowany wzór pod pierwiastkiem jest widoczny w linii 24. Sprawdzamy jeszcze zgodnie z równaniem, czy wyznaczona wartość jest mniejsza bądź równa 1. Jeżeli tak, to wiadome jest, że punkt leży wewnątrz okręgu.
Podsumowując
Po tym, jak w pętli przeanalizowana zostanie podana na wejściu liczba punktów, następuje obliczenie wartości końcowej za pomocą wzoru prezentowanego wyżej. Pole kwadratu, na którym oparte jest koło (wynosi w tym przypadku 4), zostaje przemnożone przez sumę liczby punktów w środku koła, a następnie podzielone przez liczbę wszystkich wylosowanych punktów.
Przy odpowiednio dużej liczby punktów, podanych na wejściu program pokaże bardzo dokładne przybliżenie liczbę PI do kilku cyfr po przecinku. Na przykład szacunki dla 100000 punktów są następujące:
- 3.15476
- 3.13836
- 3.13904
Jak widać, przybliżenie może nie jest zbyt dokładne, jednak pokazuje możliwości, jakie ma metoda Monte Carlo.
using System;
namespace MC
{
public class Program
{
public static void Main(string[] args)
{
Console.WriteLine("Podaj liczbę losowych punktów: ");
int counter = int.Parse(Console.ReadLine());
int inTheMiddle = 0;
double valX, valY;
Random rand = new Random();
decimal returnVal;
if (counter < 3)
Console.WriteLine("Nie można wyznaczyć przybliżonej wartości PI");
else
{
for (int i = 0; i < counter; i++)
{
valX = rand.NextDouble() * 2;
valY = rand.NextDouble() * 2;
if (Math.Sqrt((valX - 1) * (valX - 1) + (valY - 1) * (valY - 1)) <= 1)
inTheMiddle++;
}
returnVal = 4 * inTheMiddle / (decimal)counter;
Console.WriteLine("Liczba PI w przybliżeniu wynosi: " + returnVal.ToString());
}
Console.ReadLine();
}
}
}
Czy wiesz, że…
Sama metoda Monte Carlo nie byłaby tak popularna, gdyby nie fakt jej przydatności. Poniżej kilka przykładów zastosowania jej w połączeniu z komputerami:
- obliczanie całek oznaczonych
- sprawdzanie jakości i niezawodności produktów, czyli na przykład do oszacowania długości życia żarówki wolframowej
- systemy obsługi klientów, czyli przepustowość kas w sklepie lub długość oczekiwania na połączenie z infolinią
- zastosowania w fizyce, czyli rozszczepianie cząstek
- analiza danych w takich dziedzinach jak finanse
Jednym z ciekawszych zagadnień powiązanych z metodą Monte Carlo jest tak zwany problem igły Buffona, czyli problem polegający na tym, że na pewnej planszy narysowane są linie oddalone od siebie o odległość S. Na planszę upuszczane są igły o długości L (przy założeniu, że długość igły jest mniejsza niż odległość między równoległymi liniami). Eksperyment wykonywany jest poprzez rzut igłą N razy. Następnie liczone jest, ile razy igła przecięła równoległą linię. Korzystając ze wzoru (2 * długość igły * liczba wszystkich rzutów) / (odległość między równoległymi liniami * stosunek liczba rzutów przecinających równoległe linie do wszystkich rzutów) pozwala nam oszacować przybliżoną wartość liczby Pi.


Doświadczenie tego typu przedstawiane jest również na filmie poniżej!
Metoda Monte Carlo — Podsumowanie
I to już koniec. Temat nie jest łatwy, jednak opracowywanie go sprawiło wiele frajdy. Spędziłem nad nim wiele godzin, kilka wieczorów zarwałem w bibliotece lub na uczelni, jednak uważam, że było warto!
Aktualnie wiem jedno, niektóre tematy są bardzo ubogie w materiały i trzeba głęboko szukać, by wydobyć to, co najlepsze. Tak było właśnie w przypadku tematu związanego z metodą Monte Carlo.
Mam jednak nadzieję, że analiza Ci się spodobała i będziesz pogłębiał wiedzę z tych i podobnych tematów! W kolejnym, czwartym wpisie coś luźnego, opiszę swoje pomysły na temat zarządzania czasem, czyli dylatacja czasu.
Źródła
http://home.agh.edu.pl/~pernach/wyklady/index.php?action=wyklad10_1 http://kft.umcs.lublin.pl/baran/epk/modelowanie/sobol.pdf http://dotproject.net.pl/node/227 https://analizy.investio.pl/metoda-monte-carlo/ http://mst.mimuw.edu.pl/wyklady/sst/wyklad.pdf http://zif.wzr.pl/pim/2012_4_1_2.pdf http://keii.ue.wroc.pl/pracownicy/tb/Bart%C5%82omowicz%20T.%20[2011],%20Symulacja%20Monte%20Carlo%20jako%20narz%C4%99dzie%20prognozowania%20wybranych%20aspekt%C3%B3w%20rynku%20nieruchomo%C5%9Bci,%20W%20Pociecha%20J.%20(red.)%20Modelowanie%20i%20prognozowanie%20zjawisk...,%20UE%20Krak%C3%B3w.pdf http://www.deltami.edu.pl/temat/matematyka/rachunek_prawdopodobienstwa/2011/02/01/Jak_matematyk_rzuca_igla/ http://coin.wne.uw.edu.pl/~tmostowski/pliki/matlab/matlab7.pdf http://www.algorytm.org/procedury-numeryczne/calkowanie-numeryczne-metoda-monte-carlo-i.html http://prac.im.pwr.edu.pl/~agniesz/rachunek_prawd_MAEW104/Monte_Carlo_pole_obszaru_prezentacja_1.pdf https://eduinf.waw.pl/inf/alg/004_int/0005.php http://www.if.pw.edu.pl/~agatka/numeryczne/wyklad_11.pdf https://www.ue.katowice.pl/fileadmin/_migrated/content_uploads/10_02.pdf https://mfiles.pl/pl/index.php/Metoda_Monte_Carlo http://home.agh.edu.pl/~chwiej/mn/mc_2015.pdf
Newsletter
Nie przegap i dołącz już dziś do 842 osób będących w tym Newsletter! Otrzymuj co niedzielę o godzinie 20 listę kilku ciekawych tematów, które miałem okazję obserwować w mijającym tygodniu.
Tematy będą głównie techniczne, ale czasami pojawi się coś, co może wprowadzi Cię w stan zadumy i zmusi do dyskusji w szerszym gronie. Zero spamu!







13 komentarzy
Super wyjaśnienie, dzięki za ten wpis Mateusz!
1. „Główne ciało metody rozpoczyna się instrukcją warunkową, która sprawdza, czy liczba losowych punktów nie jest mniejsza od 3.” -> „if (counter < 2)"
2. Co tu się stało, dlaczego tak? ?
"float returnValFloat = 4 * float.Parse(inTheMiddle.ToString()) / float.Parse(counter.ToString());
returnVal = returnValFloat .ToString();"
Zmieniłbym więcej, ale po poprawkach:
Console.WriteLine("Podaj liczbę losowych punktów: moje");
int counter = int.Parse(Console.ReadLine());
int inTheMiddle = 0;
double valX, valY;
Random rand = new Random();
decimal returnVal;
if (counter < 3)
{
Console.WriteLine("Nie można wyznaczyć przybliżonej wartości PI");
}
else
{
for (int i = 0; i < counter; i++)
{
valX = rand.NextDouble() * 2;
valY = rand.NextDouble() * 2;
if (Math.Sqrt((valX – 1) * (valX – 1) + (valY – 1) * (valY – 1)) <= 1)
inTheMiddle++;
}
returnVal = 4 * inTheMiddle / (decimal)counter;
Console.WriteLine($"Liczba PI w przybliżeniu wynosi: {returnVal}");
}
Console.ReadLine();
3. W niektórych miejscach informacje są niejasne lub stosowane są skróty myślowe, które dla osoby czytającej mogą nie być oczywiste.
4. Poza tym ogólnie dobry wpis. W większości wszystko jest jasno wyjaśnione i można się dowiedzieć czym jest tytułowa metoda od zera. Nie słyszałem wcześniej o metodzie Monte Carlo, ani nie miałem pojęcia że jest tak szeroko stosowana. Fajnie by było zobaczyć wpis z bardziej skomplikowanym i szczegółowym jej zastosowaniem w jednej z dziedzin, które Pan wymienia w artykule.
Cześć, dziękuje za uwagi.
Refaktoryzacja bardzo dobra, w wolnej chwili się zapoznam i wprowadzę usprawnienia 🙂
Pozdrawiam, Mateusz.
Hej, ciekawy artykuł 🙂
Mam jedną uwagę: w przypadku rzeczowników policzalnych używamy określenie „liczba” zamiast „ilość”.
Poza tym świetnie się czyta.
Pozdrawiam 🙂
Cześć Krystian, dzięki za miłe słowa i oczywiście uwzględniłem Twoje uwagi co do określenia liczby zamiast ilości 🙂
Pozdrawiam, Mateusz.
Z artykuł na artykuł Twój blog mi się coraz bardziej podoba, bardzo fajny znalazłeś sposób na prowadzenie swojego miejsca w sieci. Gratuluję 🙂
Pozdrawiam,
Dariusz Gruca
http://www.DariuszGruca.pl
Cześć Dariusz, bardzo miło, że doceniasz moją twórczość 🙂
Postaram się produkować treści częściej i z jeszcze większym profesjonalizmem.
Pozdrawiam, Mateusz.
Dla mnie nowość! Nie słyszam o tym wcześniej mimo, że skończyłam Politechnikę! Ciekawy blog, fajnie, że na niego trafiłam, będę odwiedzać Cię wcześniej 🙂
Cześć, bardzo mnie cieszy to, że artykuł okazał się pomocny! 🙂
Pozdrawiam, Mateusz.
Rysunek 3 wskazuje na to, że środek okręgu i kwadratu zawierają się w początku układu współrzędnych. W równaniu okręgu a,b to współrzędne środka, zatem nie ma mowy żeby a i b były równe 1. (chyba że czegoś nie doczytałem)
„Wystarczy zgodnie z regułą opisywaną na początku artykułu zebrać wszystkie punkty, które trafiły w okrąg, przemnożyć te punkty przez pole kwadratu i na końcu podzielić wynik przez ilość wszystkich pomiarów, które zostały użyte.”
Oczywiście rozumiem, że to pewien skrót myślowy, niemniej – jeśli już (potocznie) to punkty trafiły w KOŁO, nie okrąg. To takie upierdliwe uwagi.
Prócz tego artykuł bardzo fajnie napisany, pisz dalej 😀
Dziękuję za uwagi, staram się nie stosować skrótów myślowych. 🙂 dziękuję za uwagi, wprowadzę stosowne sprostowania!
Pozdrawiam, Mateusz Rus.
Świetny blog !!! Ciekawe z punktu widzenia matematyka tematy. Cieszę się że dowodzisz na każdym kroku, że matematyka ma także zastosowanie w praktyce a nie jest tylko suchą teorią. Bardzo dobrze czyta się kolejne wpisy mimo że materia nie jest trywialna.
Aha i jeszcze jedno – materiały w cotygodniowym mailingu trzymają wysoki poziom. Pozdrawiam
Dziękuje Krzysztof za miłe słowa, mam w planach rozwijać jeszcze kilka tematów matematycznych, o których nie uczą w szkole.
Pozdrawiam, Mateusz!