#16. Metody numeryczne – wprowadzenie

Znów coś związanego z matematyką. Przed Tobą metody numeryczne! Nie uciekaj, proszę, tylko przeczytaj ten artykuł do samego końca. Co prawda, temat metod numerycznych nie należy do najłatwiejszych, ale postaram się go rozłożyć na czynniki pierwsze. Mam nadzieję, że dzięki temu będzie to zagadnienie łatwiejsze do przyswojenia.

Poruszę następujące zagadnienia:

• Czym są metody numeryczne?
• Jak je kategoryzujemy?
• Jakie są z nimi związane błędy?

Połączenie matematyki z komputerem to coś fascynującego. Metody numeryczne zapewne kojarzą Ci się z nudnym i trudnym przedmiotem na studiach, gdzie Twoim zadaniem było stworzenie programu do liczenia całek. Pokażę Ci, że tego typu zagadnienia mogą być naprawdę fajne.

Wszystko po kolei. Zaczynajmy!

Wprowadzenie

Metody numeryczne to dla studenta jeden z tych przedmiotów, który budzi postrach i potrafi przyspieszyć proces siwienia włosów. Matematyka i masa dziwnych wzorów oraz zabiegów programistycznych opakowane w dziwnie brzmiący tytuł. Tak krótko można zdefiniować metody numeryczne. Na temat matematyki napisałem mikropost na grupie facebookowej, gdzie przedstawiłem ją jako ciekawy przedmiot ścisły, którego piękno nie zostało nam zaprezentowane przez nauczyciela/wykładowcę. 

Z racji tego, że metody numeryczne są silnie powiązane z matematyką stąd awersja większości studentów do przedmiotu. Warto mieć jednak na uwadze to, że we współczesnym świecie posiadanie takich narzędzi analitycznych w rękach programistów to dodatkowy atut.

Postaram się trochę rozluźnić atmosferę i pokazać ciekawe zagadnienia z fragmentami kodu i grafikami. 

Informacje ogólne

Jak podaje definicja, metody numeryczne to sposoby rozwiązywania problemów matematycznych za pomocą operacji na liczbach. Wszystkie popularne języki programowania udostępniają biblioteki do tego celu. Jedno na pewno trzeba powiedzieć na początku — wyniki z obliczeń metodami numerycznymi nie są wynikami dokładnymi i podczas pracy nad problemem z góry zakładamy dokładność obliczeń. Skoro wyniki nie są dokładne, to wiemy też, że metodami numerycznymi nie będziemy obliczać czegoś w sposób analityczny, czyli za sprawą gotowego wzoru. 

Może się też okazać, że wzór w zasadzie jest gotowy, ale proces obliczeniowy będzie tak czasochłonny, że lepiej będzie wynik oszacować szybciej z pewnym błędem.

Do problemów idealnie nadających się pod metody numeryczne są:

• całki
• wielomiany wyższego stopnia niż 2
• skomplikowane równania liniowe i różniczkowe
• zaawansowane obliczenia fizyczne i chemiczne  
• symulacje zjawisk przyrodniczych oraz społecznych

Proces modelowania matematycznego

Warto pokusić się o pewien model matematyczny, który pokaże, w którym miejscu procesu pojawiają się obliczenia za pomocą metod numerycznych. Aby zacząć pisać oprogramowanie, musi być dopracowanych kilka rzeczy. Po pierwsze musimy mieć obiekt, który będzie ulegał pomiarom (ważony przedmiot, samochód, telewizor, czy zderzane cząsteczki fizyczne). Następnie model fizyczny (waga, komputer, Wielki Zderzacz Hadronów). Gdy już mamy co i czym mierzyć to trzeba zaproponować model matematyczny. Wzory, metody obliczeń i pomiarów. Po tych trzech krokach wpiąć w model możemy metody numeryczne i końcowy program komputerowy.

Błędy numeryczne

Skoro metody numeryczne nie zajmują się problemami analitycznymi z gotowymi wzorami matematycznymi, to znaczy jedno — musimy liczyć się z szacowaniem. Szacowanie natomiast wiąże się z błędami podczas działania algorytmu.

Błędów związanych z metodami numerycznymi jest dużo i czasami się na siebie nakładają. Warto je mieć jednak na uwadze pracując jako programista. Niezależnie czy pracuje się na niskim, czy wysokim poziomie. Może na nie trafić zarówno osoba pisząca sterowniki, jak i programista web, który pisze kod w JS.

Poniżej każdy z problemów omówiony bardziej szczegółowo.

Błąd ludzki

Przedstawiłem metody numeryczne jako operacje matematyczne na liczbach i pokazałem problemy, jakie możemy rozwiązywać dzięki nim. Czas na prosty przykład dotyczący błędu człowieka. Pokaże, jak bardzo duże znaczenie w nawet najprostszych działaniach mają typy danych. Program poniżej ma jedno proste zadanie, podzielić wartość jeden przez iterator, dodać do tej wartości X i przypisać do zmiennej. 

Zarówno Program numer 1, jak i Program numer 2 mają zmienną X typu float. Również w jednym i drugim programie pętla for ma iterator zdefiniowany jako int. Jedyną różnicą jest zapis jedynki. Pierwszy program wartość 1, która jest dzielona, traktuje, jako zmienną typu int. Drugi program natomiast jedynkę ma zapisaną jako float w postaci 1.0f. 

Mała zmiana a wynik jest różny. Dla pierwszego przykładu będzie to po prostu 1, ponieważ dzielenie zawsze będzie zaokrąglane w dół do pełnej liczby całkowitej. W tym przypadku im mniejszy ułamek, tym bliżej zera. Drugi przypadek to już dzielenie do 6 miejsc po przecinku i wynik takich operacji w pętli wyniesie 9.094314!

// PROGRAM NUMER 1
using System;

namespace Suma
{
    class Program
    {
        static void Main(string[] args)
        {
            float x = 0;

            for (int i = 1; i < 5000; i++)
            {
                x = x + 1 / i;
            }

            Console.WriteLine("X wynosi: " + x.ToString());
            Console.ReadLine();
        }
    }
}



// PROGRAM NUMER 2
using System;

namespace Suma
{
    class Program
    {
        static void Main(string[] args)
        {
            float x = 0;

            for (int i = 1; i < 5000; i++)
            {
                x = x + 1.0f / i;
            }

            Console.WriteLine("X wynosi: " + x.ToString());
            Console.ReadLine();
        }
    }
}

Błąd zaokrąglenia

Jest to jeden z podstawowych błędów podczas obliczeń matematycznych często spotykanych w wielu językach programowania. Dotyczy on zazwyczaj zmiennych typu float czy double. Na dwóch grafikach poniżej zaimplementowałem jednolinijkowy kod JavaScript. Użyłem funkcji o nazwie alert(). W pierwszym przypadku zrobiłem sumę liczb 0.1 oraz 0.2. W drugim przypadku sprawdziłem, czy 0.1 + 0.2 równa się 0.3.

Wyniki zaskakują! 

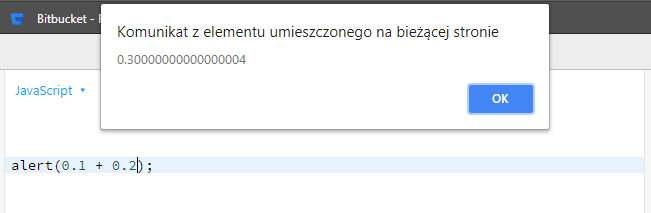
Dlaczego jednak program zachował się w tak nielogiczny dla człowieka sposób? Tu przychodzi z pomocą wiedza na temat zapisu liczb rzeczywistych za sprawą komputera. Liczba zapisywana jest jako złożenie dwóch innych liczb — mantysy m oraz cechy c (nazywana też wykładnikiem). Mantysę możemy przedstawić tak jak na poniższym wzorze. 

X to liczba całkowita ze znakiem, n natomiast reprezentuje ilość bitów mantysy. Gdy już wiemy, że mantysa jest ułamkiem, możemy przejść do wzoru na liczbę rzeczywistą. 

M to mantysa omawiana wyżej, p to podstawa. Dla systemu dziesiętnego będzie to 10, dla binarnego 2, ósemkowego 8 i tak dalej. Ostatnią zmienną jest c, która jest liczbą całkowitą.

Wzory zazwyczaj mało komu coś mówią, dlatego na tym się zatrzymajmy. Miej jednak na uwadze, że mantysa to liczba w postaci ułamka a jak wiemy z matematyki, ułamki nie zawsze są skończone. Stąd w wielu przypadkach liczba zostaje zaokrąglona do pewnej ilości miejsc po przecinku. Chcę od razu zaznaczyć, że temat liczb rzeczywistych, mantysy i standardów z tym związanych to ogromne zagadnienie i napisałem o tym osobny artykuł. 

Błąd obcięcia

Jest to błąd związany z ograniczeniem pewnego bardzo długiego ciągu znaków lub też ciągu nieskończonego do pewnej skończonej liczby znaków. Bardzo dobrym przykładem jest zamiana liczb zmiennoprzecinkowych. Liczbę 0.3 reprezentuje wartość binarna z okresową częścią 0011. Zapisać możemy to jako  .01(0011).

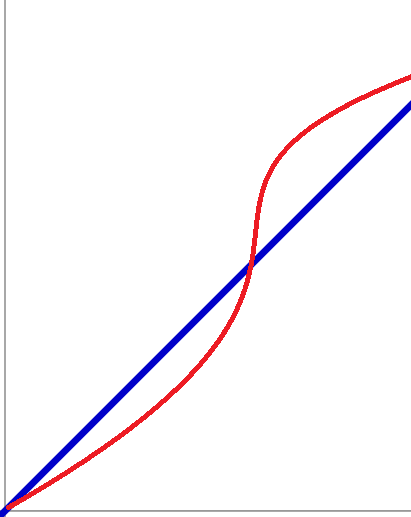
Do błędów też należy aproksymacja (przybliżenie). Dla przykładu mogę podać aproksymacje funkcji nieliniowej za pomocą funkcji liniowej.

Błąd danych wejściowych

Błędem danych wejściowych możemy nazwać sytuację, gdy dane, które dostarczane na wejście są błędne lub zbyt mało dokładne. Dzieje się to w sytuacji, gdy urządzenie do pomiaru jest źle skalibrowane, zostało uszkodzone lub ma zbyt małą czułość czujników.

Dzieje się tak podczas pomiarów odległości, wagi czy prędkości. 

Błąd modelu

Problem dotyczy złej konstrukcji algorytmu. Problemem tu jest błędne założenie, które nie do końca wynika z błędu programisty. Teoretycznie kod może działać poprawnie w 90% przypadkach jednak dla wybranych maszyn, danych wejściowych lub założeń może pokazywać błędne wyniki, lub szacowanie może trwać bardzo długi okres.

Reasumując

Jak widać, błędów związanych z metodami numerycznymi jest sporo i czasami się na siebie nakładają. 

Zdecydowałem się pójść na kompromis w kilku akapitach  i omówiłem temat tylko połowicznie. Daj znać w komentarzu, czy wolisz czytać artykuł, który byłby ogromny i poruszałby każdą kwestię bardzo szczegółowo. Czy może forma taka jak powyżej jest w porządku i kolejne akapity warto byłoby rozwinąć w osobnych artykułach? Jednym z pierwszych, który potrzebuje rozwinięcia to błąd zaokrąglenia i cały artykuł na temat liczb rzeczywistych! 

Podsumowanie

Widzisz, nie taki diabeł straszny jak go malują. Wszystko jest kwestią nastawienia i podejścia do problemu. Oczywiście, to o czym tu napisałem dziś, jest tylko informacją ogólną. Sądzę, że można spokojnie podzielić ją na kilka osobnych. Mam nawet taki plan, by pochylić się bardziej szczegółowo nad kilkoma poruszonymi tu zagadnieniami. Wszystko w swoim czasie. 

A już w następnym wpisie poruszę temat kodowania Unicode.

Źródła

http://www.rose.pwr.wroc.pl/met_numer/MN_notatki.pdf
http://home.agh.edu.pl/~horzyk/lectures/wdi/WDI-B%C5%82%C4%99dyNumeryczne.pdf
http://wazniak.mimuw.edu.pl/index.php?title=Metody_numeryczne
http://galaxy.agh.edu.pl/~chwiej/mn.html
https://www.l5.pk.edu.pl/images/skrypty/Metody_numeryczne_1
http://bc.pollub.pl/Content/1370/metody.pdf
https://fizyka.umk.pl/~jkob/mn
http://th-www.if.uj.edu.pl/zfs/gora/metnum17/wyklad01.pdf
https://fizyka.umk.pl/~wj/EDU/PMN/wpmn_new_3.pdf
https://www.mat.umk.pl/documents/27659/27763/prezentacjaBZ.pdf/e6f6232c-04f5-4690-a5fc-97a90a52a978
https://www.l5.pk.edu.pl/~awosatko/INFTRA/bledy_w01INF.pdf 

Newsletter

Nie przegap i dołącz już dziś do 841 osób będących w tym Newsletter! Otrzymuj co niedzielę o godzinie 20 listę kilku ciekawych tematów, które miałem okazję obserwować w mijającym tygodniu.

Tematy będą głównie techniczne, ale czasami pojawi się coś, co może wprowadzi Cię w stan zadumy i zmusi do dyskusji w szerszym gronie. Zero spamu!